This test probes a number of code/method properties. The initial setup is particularly simple, and on a Cartesian grid can be set up with essentially perfect symmetry, to floating point precision. The shocks generated are models, being the parameters from the standard Sod test, but here with reflecting boundaries all around, the simulation is allowed to continue for many crossing times.

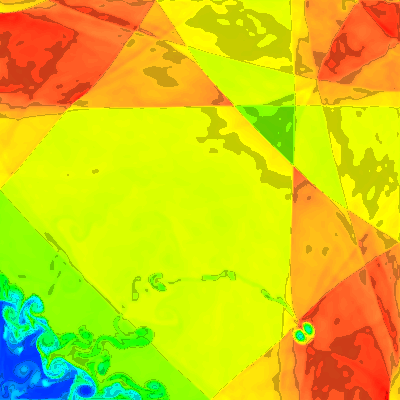
Shocks reflecting from the origin eventually generate a free standing double 2-D vortex that is free to wander over the domain and is not dissipated by crossing shocks. As the origin of the vortex is a cavity in an unstable contact discontinuity, the path and destiny of the vortex is extremely sensitive to a number of factors.

Firstly, floating-point 'noise', residual errors from the repeated application of non-linear operations can accumulate and eventually break the perfect symmetry of the intial conditions. Without specific care to control round off errors this noise will be present even in symmetric sweep codes.

Secondly, if the standard asymmetric split sweeps are applied, the small assymmetry generated by the intial sweep (x or y) results in an asymmetric grid that will evolve with a small bias from then on. In this simulation that leads to the double vortex drifting in quite different directions over the grid. Only symmetric sweep operations will result in the double vortex favoring neither the left or right and instead remaining on the diagonal.

Thirdly, related to the first, the eventual speed and the detailed distributions at the final step are so sensitive, that even the same code running on two different computer architectures can result in different final conditions. This can be understood both in terms of the infintesimal coordinate differences of the grid cells owing to differences in floating point representations, and any differences in the operating system libraries of mathematical routines.

To demsonstrate how Fyris behaves under all these options requires a large number of tests, presented below. First the results from a standard run, with default settings. Then variations with:

• the sweep order reversed,
• using a symmetric form of split sweeps,
• a symmetric sweep model with deliberate initial assymmetry,
• standard runs on comparison operating systems/architectures.

Of these, four are presented with animations and snapshots of the final state. The others are presented simply as final state density snapshots.

Initial conditions

Adiabatic index

• Gamma = 1.4

Inside region: y < (0.15 - x)

• Density = 0.125
• Pressure = 0.140
• Velocity = 0.000

Outside region

• Density = 1.000
• Pressure = 1.000
• Radial Velocity = 0.000

Grid

• Domain: 0.0 < x <1.0, 0.0 < y < 1.0
• 400 x 400 cells
• All boundaries are reflecting.

Algorithm settings

• CFL number: 0.8, initial step 0.4 (standard)
• Flattening: minimum 0.0, maximum 1.0 (standard)
• Alpha = 0.001 (standard)

Ending condition

• Time, t = 2.5

The code and configuration files for Fyris to run the 2D Implosion problem will be available soon.

Test models

These models were run: all MacOS X Quad G5, gcc -fast, Big Endian, except models 4a - 4b.

1. Standard Fyris Alpha Strang split sweeps, alternating: get data 0, X - Y sweeps, store results 1, get data 1 Y - X sweeps, store results 2 ...

   • Model 1a ran with the x-sweep first
   • Model 1b ran with the y-sweep first
2. Mean Sweeps (MS) two sweeps per update are performed, retaining intermediate results and averaging at the end: get data 0, X - Y sweeps, keep results 1x, get data 0 Y - X sweeps, keep results 1y, average : 0.5*(results 1x + results 1y) and store results 1, ...

3. Mean Sweeps with a slightly (~1%) asymmetric initial condition, where the boundary is smoothed.

4. Standard sweeps, various other operating systems:
   • a) Dell, Windows XP Pro, AMD Turion mobile, Cygwin, gcc -O3, Little Endian
   • b) Solaris 10, AMD Opteron, 8 processor, sun cc -fast, 64 bit Little Endian

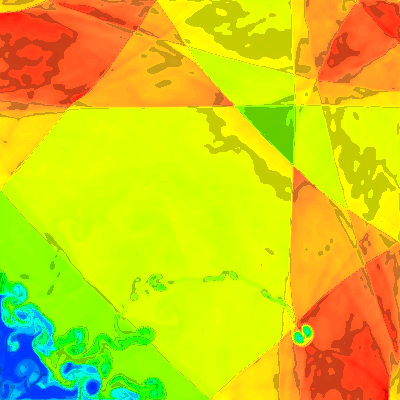
In principle, the initial conditions are symmetric, ie d[j][i] == d[i][j]. Normal Strang splitting starts out with a non-symmetric initial x-sweep, so that the subsequent y-sweep sees a grid that is no longer symmetric w.r.t the initial x-sweep. In this problem the destiny of the unstable interface and the generated double vortex depend sensitively on the symmetry of the calculation. In the Linska and Wendroff results, the symmetric, unsplit, codes maintained symmetry throughout the simulation, leaving the vortex on the diagonal axis. PPM and vh1, (like Fyris) normally use split sweeps. Globally these codes perform well, but as the symmetry is broken in the early sweeps the late time symmetry is not present, and the vortex is no longer found on the diagonal. Starting with an x-sweep results with the vortex drifting to the upper left of the diagonal. Simply reversing the order of the initial sweeps from X-Y to Y-X, gives the same vortex drifted off to the lower right.

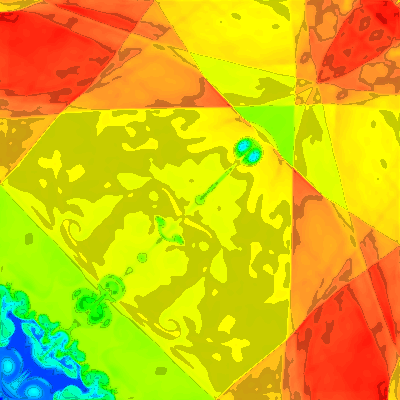
The mean sweep method requires more intermediate memory (2 times in 2D), but is symmetric. If the initial conditions are symmetric then the symmetry will be preserved. If the initial conditions are slightly asymmetric then the grid will evolve asymmetricly.

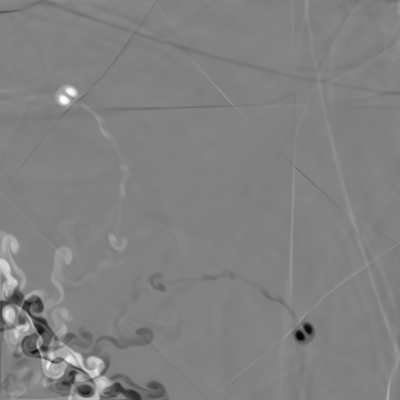
To display the symmetry, a symmetric difference in density d_sym = d[j][i] - d[i][j] has been computed for each frame. If the density field is precisely symmetric (influencing floating point precision) then d_sym = 0.0 everywhere. If symmetry breaks then d_sym shows positive and negative values mirrored about the grid diagonal.

Results

QuickTime movies: models 1-3, 0.01 time steps, 250 frames each.

Density at t = 2.5

min = 0.0  max = AutoScale

 Symmetric density d[j][i] - d[i][j] at t = 2.5

min = AutoScale  max = AutoScale