2-D Gresho vortex tests
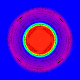
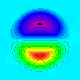
The Gresho vortex is a 2-D pattern where the cetrifugal force are matched by pressure gradients, resulting in a stable time-independent vortex. This 2-D L&W test consists of single 2-D vortex on a range of grid resolutions. One test models a stationary vortex, and the second test advects the vortex across three diameters. The code and configuration files plus output for Fyris to run the 2-D advection convergence test will be available soon.
The vortex is defined here by:
Initial conditions
- A vortex initially centred about (0.5, 0.5), outer radius r = 0.40
- Adiabatic index: Gamma = 5/3
- Density = 1.0 everywhere
Pressure
- r <= 0.2; P(r) = 5.0 +25/2 r^2
- 0.2 < r <= 0.4 ; 9 – 4 ln 0.2 + 25/2 r^2 – 20 r + 4 ln r
- 0.4 < r ; 3 + 4 ln 2
Azimuthal velocity v_phi
- r <= 0.2; v_phi(r) = 5r
- 0.2 < r <= 0.4 ; v_phi(r) = 2 – 5r
- 0.4 < r ; v_phi(r) = 0.0
Resulting 2D vorticity, V_yx (r)
- r <= 0.2; V_yx(r) = 10.0
- 0.2 < r <= 0.4 ; V_yx(r) = 2/r - 10.0
- 0.4 < r ; V_yx(r) = 0.0
The stationary vortex
Ending condition
- Time, t = 3.0
Grid
- Domain: x = 0 -> 1.0, , y = 0 -> 1.0
- Boundary conditions are free or natural boundaries
- Runs are made on a 20x20 (a20), 40x40 (a40), 60x60 (a60) and 80x80 (a80) grid
Hydrodynamics settings
- CFL number: 0.8, initial step 0.4 (standard)
- Flattening: minimum 0.0, maximum 1.0 (standard)
Errors and L1 norms are computed over a unit square centred on (0.5, 0.5) at t = 3.0.
Results
The stationary vortex at t = 3.0
| Stationary | Density L1 % | Vorticity L1 % | Total KE Error % | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Code | a20 | a40 | a60 | a80 | a20 | a40 | a60 | a80 | a20 | a40 | a60 | a80 | ||
| Fyris | 0.150 | 0.0276 | 0.0181 | 0.0144 | 26.4 | 14.5 | 11.1 | 8.89 | 11.6 | 1.85 | 0.733 | 0.383 | ||
| CFLFh | 0.22 | 0.16 | 22 | 20 | 0.2 | 0.4 | ||||||||
| JT | 0.56 | 0.22 | 89 | 45 | 55.2 | 18.3 | ||||||||
| LL | 2.27 | 0.23 | 71 | 44 | 65.6 | 26.1 | ||||||||
| CLAW | 0.33 | 0.10 | 50 | 28 | 29.9 | 6.1 | ||||||||
| WAFT | 0.24 | 0.07 | 47 | 26 | 7.7 | 5.7 | ||||||||
| WENO | 0.35 | 0.06 | 38 | 27 | 30.9 | 3.7 | ||||||||
| PPM | 0.20 | 0.04 | 25 | 13 | 9.1 | 0.8 | ||||||||
| VH1 | 0.15 | 0.04 | 26 | 15 | 9.6 | 1.2 | ||||||||
|
a20 Density (0.996072, 1.00688) |
a20 Pressure (5.05753, 5.79528) |
a20 Vorticity (-4.19047, 11.0509) |
a20 Velocity_x (-0.795881, 0.795881) |
|
a40 Density (0.998955, 1.00132) |
a40 Pressure (5.01343, 5.77697) |
a40 Vorticity (-4.45904, 10.4167) |
a40 Velocity_x (-0.899295, 0.899295) |
|
a60 Density (0.999382, 1.00105) |
a60 Pressure (5.00564, 5.77629) |
a60 Vorticity (-4.92575, 10.3582) |
a60 Velocity_x (-0.928645, 0.928645) |
|
a80 Density (0.999134, 1.00096) |
a80 Pressure (5.00309, 5.77541) |
a80 Vorticity (-5.19555 , 10.3471) |
a80 Velocity_x (-0.941055, 0.941055) |
|
min |
|||
The moving vortex
Same as the stationary vortex, with a global v_x = 1.0 drift velocity added to the whole grid, on top of the initial vortex velocity field.
Ending condition
- Time, t = 3.0
Grid
- Domain:0.0 < x < 4.0, 0.0 < y <1.0
- Boundary conditions are free or natural boundaries.
- Runs are made on a 20x80 (b20), 40x160 (b40), 60x240 (b60) and 80x320 (b80) grid.
The vortex drifts from the left to the right. At t = 3.0 the vortex should be centred on (3.5,0.5).
Errors and L1 norms are computed over a unit square centred on the expected vortex centre at t = 3.0.
Results
The vorticity is estimated from the discrete grid by the central finite difference:
vorticity[i,j] = 0.5*{(vy[i+1, j]-vy[i-1,j])/dx - (vx[i, j+1]-vx[i,j-1])/dy}
Moving vortex at t = 3.0
| Stationary | Density L1 % | Vorticity L1 % | Total KE Error % | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Code | b20 | b40 | b60 | b80 | b20 | b40 | b60 | b80 | b20 | b40 | b60 | b80 | ||
| Fyris | 0.649 | 0.568 | 0.104 | 0.042 | 62.08 | 56.47 | 18.97 | 14.52 | 2.072 | 0.031 | 0.039 | 0.003 | ||
| CFLFh | 1.12 | 0.72 | 145 | 83 | 12.8 | 0.1 | ||||||||
| JT | 0.81 | 0.22 | 100 | 52 | 42.8 | 22.1 | ||||||||
| LL | 0.65 | 0.49 | 88 | 60 | 71.6 | 30.9 | ||||||||
| CLAW | 0.72 | 0.29 | 65 | 37 | 39.9 | 8.3 | ||||||||
| WAFT | 0.87 | 0.77 | 65 | 62 | 1.3 | 12.6 | ||||||||
| WENO | 0.37 | 0.43 | 48 | 40 | 31.6 | 4.0 | ||||||||
| PPM | 1.1 | 0.42 | 93 | 36 | 4.9 | 1.0 | ||||||||
| VH1 | 0.8 | 0.66 | 65 | 55 | 11.7 | 1.2 | ||||||||
 max)
max)b20 Density
(0.980141, 1.02896)
b20 Vorticity
(-4.46422, 16.7204)
b40 Density
( 0.977118, 1.01814)
b40 Vorticity
(-5.56746, 11.4596)
b60 Density
(0.995089, 1.00389)
b60 Vorticity
(-5.23023, 11.0323)
b80 Density
(0.997859, 1.00166)
b80 Vorticity
(-5.1049 , 10.974)
b20 Pressure
(5.17565 , 5.8355)
b20 Velocity_x
(0.140607, 1.86165)
b40 Pressure
(5.1033, 5.81134)
b40 Velocity_x
(0.34762, 1.6984)
b60 Pressure
(5.00907, 5.78504)
b60 Velocity_x
(0.0961467, 1.90601)
b80 Pressure
(5.00332, 5.78039)
b80 Velocity_x
(0.0770731, 1.9277)